Турнир Архимеда. Московская математическая регата. 10 класс

Московская математическая регата
10 класс

1 марта 2008 года состоялась математическая регата 10-х классов, в которой приняли участие 62 команды. Помимо команд из Москвы в регате участвовали школьники из Московской области (Дзержинский, Долгопрудный, Королев), а также из Костромы, Переславля и Санкт-Петербурга.

Регата проходила, как всегда, в Московском городском дворце детского (юношеского) творчества (директор Д. Монахов) при финансовой поддержке Департамента образования г. Москвы, организационной и технической поддержке Московского центра непрерывного математического образования (директор — И. Ященко).

По сложившейся традиции Московских регат каждый участник и руководитель команды по окончании регаты получал небольшую брошюру с условиями и решениями задач только что прошедшей регаты, подготовленную коллективом редакции «Архимед» под руководством П. Чулкова.

В подготовке и проведении регаты приняли участие около сорока человек, из которых особо отметим В. Арнольда, С. Голубева, Е. Горскую, В. Гуровица, А. Заславского, Д. Селегея, Б. Френкина и А. Хачатуряна.

Дипломами Турниров Архимеда и математической литературой (традиционно предоставляемой МЦНМО) были награждены 10 команд. Абсолютно лучший результат показала одна из команд СУНЦ МГУ, получившая диплом I степени.

Полные итоги регаты опубликованы на сервере МЦНМО (http://www.mccme.ru/olympiads). Там же можно найти материалы регат предыдущих лет, которые регулярно публикуются и на страницах газеты «Математика». Подробно о том, как проводятся математические регаты, — см. сборник «Московские математические регаты» (Cост.: А.Д. Блинков, В.М. Гуровиц, Е.С. Горская. М.: МЦНМО, 2007).

Как обычно, часть заданий придумывалась авторами специально для этой регаты, а остальные являются математическим фольклором или взяты из популярной математической литературы. Тексты решений опубликованы в том виде, в котором они готовились для работы жюри.

Условия задач

Первый тур

(10 минут; каждая задача — 6 баллов)

1.1. Известно, что | a + b | + | a – b | ≤ 2.

Докажите, что a² + b² ≤ 2.

1.2. Найдите гипотенузу прямоугольного треугольника, если сумма длин его катетов равна 12, а сумма косинусов острых углов равна

1.3. Можно ли разрезать куб на пять треугольных пирамид?

Второй тур

(15 минут; каждая задача — 7 баллов)

2.1. Квадратный трехчлен f(x) = x² + аx + b имеет два корня, один из которых лежит внутри отрезка [0; 1], а другой — вне этого отрезка. Определите знак f(b).

2.2. На диагонали АС выпуклого четырехугольника АВСD выбрана точка О так,
что OC = OD и CОD = 90°.
Известно также, что AОB = 110° и точка О равноудалена от прямых DA, AB и BC. Найдите углы четырехугольника.

2.3. В верхнем углу таблицы 11 ´ 11 стоит число 1, а остальные клетки пусты. Сережа заполняет таблицу по следующему правилу: если в какой-то клетке стоит число x, то он ставит в любую соседнюю (по стороне) пустую клетку либо число 4x, либо число (x – 12), либо число (x + 3). Сможет ли он добиться того, чтобы сумма всех чисел таблицы стала равной нулю?

Третий тур

(20 минут; каждая задача — 8 баллов)

3.1. Найдите наименьшее значение выражения (x + y)(x + z), где x, y и z — положительные числа и xyz(x + y + z) = 1.

3.2. Главные диагонали шестиугольного сечения куба пересекаются в одной точке. Обязательно ли это сечение проходит через центр куба?

3.3. Найдите все натуральные числа, которые в 11 раз больше суммы своих цифр.

(25 минут; каждая задача — 9 баллов)

4.1. Известно, что для положительных чисел а, b и c выполняется неравенство

Докажите, что a + b + c ≥ 3abc.

4.2. Вершина С прямого угла треугольника АВС лежит внутри окружности с центром О и радиусом R, проходящей через концы гипотенузы АВ, СН — высота треугольника АВС.
На прямой АВ взята точка K так, что KН = ОН. Найдите СK.

4.3. При каких натуральных значениях n числа (nⁿ + 1) и ((2n)²ⁿ + 1) являются простыми одновременно?

Пятый тур

(15 минут; каждая задача — 7 баллов)

5.1. Существует ли такая функция f(t), где t [–1; 1], что для всех x [0; π] выполняется равенство f(cos x) = sin x?

5.2. Три высоты остроугольного треугольника пересекаются в точке H, которая делит одну из высот пополам, а другую в отношении 2 : 1, считая от вершины. В каком отношении точка H делит третью высоту?

5.3. На дискотеку пришло некоторое количество мальчиков и девочек, всего — не более 40 человек. Каждая девочка бросила взгляд на каждого знакомого мальчика, а каждый мальчик бросил взгляд на каждую незнакомую ему девочку. Всего было брошено 117 взглядов. Сколько мальчиков могло быть на этой дискотеке?

1.1. Способ I. На координатной плоскости aOb неравенство | a + b | + | a – b | ≤ 2 задает квадрат с вершинами в точках (1; 1); (–1; 1); (–1; –1) (1; –1), а неравенство a² + b² ≤ 2 — круг с центром (0; 0) и радиусом (рис. 1). Поскольку квадрат вписан в круг, то для всех (а; b), удовлетворяющих первому неравенству, выполняется и второе неравенство.

Рис. 1

Способ II. Так как

2 ≥| a + b | + | a – b | ≥ | (a + b) + (a – b) | = 2| a |, то | a | ≤1.

Аналогично, 2 ≥| a + b | + | b – a | ≥ | (a + b) + (b – a) | = 2| b |, то есть | b | ≤1.

Тогда a² ≤ 1 и b² ≤ 1, следовательно, a² + b² ≤2.

Способ III. Возведем обе части данного неравенства в квадрат:

| a + b | + | a – b | ≤ 2 (| a + b | + | a – b |)² ≤4
(a + b)² + 2| a + b || a – b | + (a – b)² ≤ 4
2a² + 2b² + 2| a² – b² | ≤ 4 a² + b² ≤ 2.

Способ IV. Пусть | a + b | = x ≥ 0, | a – b | = y ≥ 0.

Тогда

Докажем, что при x ≥ 0, y ≥0 из неравенства x + y ≤ 2 следует неравенство

Это можно сделать по-разному. Например:

• От противного. Пусть это не так, тогда

— противоречие.

• Графически. Система неравенств задает на координатной плоскости треугольник с вершинами в точках (0; 0); (0; 2); (2; 0), который целиком принадлежит кругу с центром (0; 0) и радиусом R = 2. Этот круг является графиком доказываемого неравенства (рис. 2).

Рис. 2

1.2.

Пусть С — вершина прямого угла треугольника АВС; ВС = а, АС = b, AB = c (рис. 3).

Рис. 3

Способ I. Так как a = ccos B, b = ccos A, то a + b = c (cos A + cos B). По условию то есть

Способ II. Так как cos A + cos B = cos A + cos (90° – A) = cos A + sinA =

то равенство, указанное в условии, достигается тогда и только тогда, когда A = B = 45°. Тогда а = b = 6,

1.3. Да, можно.

Пусть дан куб ABCDEFGH. Искомые пять пирамид — DCAH, EAFH, BACF, GCFH и FACH (рис. 4).

Рис. 4

2.1. f(b) < 0.

Способ I. График данного трехчлена — парабола, ветви которой направлены вверх. Заметим, что

f(b) = b² + аb + b = b(а + b + 1) = f(0)f(1).

Из условия задачи следует, что числа f(0) и f(1) имеют разные знаки (рис. 5,а и б). Следовательно, f(b) < 0.

Рис. 5

1. Если x₂ < 0, то b = x₁x₂ < 0 и x₂ < b. Следовательно, b(x₂; x₁), то есть f(b) < 0 (см. рис. 5,а).
2. Если x₂ > 1, то b = x₁x₂ и x₂ > b. Следовательно, b(x₁; x₂), то есть f(b) < 0 (см. рис. 5,б).

2.2. A = 50°, B = 90°, C = D = 110°.

Пусть Р, Q и R — основания перпендикуляров, опущенных из точки О на прямые DA, AB и BC соответственно (рис. 6). Тогда Р и Q — внутренние точки сторон AD и АВ соответственно, поскольку

AОD = 90°, AОB = 110°.

Рис. 6

По условию | OP | = | OQ | = | OR |. Используя признак равенства прямоугольных треугольников по гипотенузе и катету, получим:

∆OPA = ∆OQA;
∆OQB = ∆ORB; ∆ORC = ∆OPD.

Значит, при вершине О, помимо прямого угла СОD, есть три пары равных углов, следовательно,

2AOQ + 2QOB + 2ROC + COD = 360°.

Учитывая, что

2AOQ + 2QOB = 2AOB = 220°,

получим, что ROC = 25°.

Отметим, что если точка R лежит на продолжении стороны ВС, то

2AOQ + 2QOB = 2AOB = 270°,

что противоречит условию.

Следовательно, RCО = PDО = 65°, тогда

C = D = 110°;
A = 2РAO = 2РOD = 2ROC = 50°;
B = 360° – (A + C + D) = 90°.

Комментарий. Подсчет углов можно провести иначе, если использовать тот факт, что точка О — центр окружности, касающейся прямых DA, AB и BC, то есть О — точка пересечения биссектрис углов А и В данного четырехугольника.

Пусть BAО = DAO =α, ABО = CBO =β, BCО = ADO =γ. Тогда, используя теоремы о сумме углов треугольника и о внешнем угле треугольника, составим систему уравнений:

Решив ее (проще всего способом сложения), получим: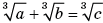

Отсюда сразу следует ответ, приведенный выше.

2.3. Нет, не сможет.

Заполнение таблицы начинается с числа 1, и все числа, поставленные Сережей, имеют при делении на 3 остаток 1. Действительно, прибавление числа 3 или вычитание числа 12, очевидно, не меняет остатка от деления на 3, а поскольку 4x = x + 3x, то и эта операция сохраняет остаток от деления на 3.

Следовательно, сумма S всех чисел таблицы имеет вид: S = 3n +121 = (3n +120) + 1, где nZ. Таким образом, число S также дает остаток 1 при делении на 3, то есть S ≠ 0.

3.1. 2.

Способ I. Так как x > 0, y > 0, z > 0, то xyz(x + y + z) = 1
yz(x² + xy + xz) = 1 x² + xy + xz =

Тогда

Равенство достигается, например, если

Способ II. Пусть

тогда

Равенство, заданное в условии задачи, примет вид:

Докажем, что все сомножители в его левой части — положительные числа. Так как произведение и четвертый множитель положительны, то отрицательными могут быть только ровно два из первых трех множителей. Пусть, например, Сложив эти неравенства почленно, получим, что а<0 — противоречие. Аналогичный результат получится, если рассмотреть любую другую пару сомножителей.

Следовательно, существует треугольник со сторонами а, b и с. Найдем его площадь по формуле Герона:

С другой стороны,

Следовательно, (x + y)(x + z)≥2, отсюда наименьшее значение равно 2. Найденные ваше значения y = z = 1 и удовлетворяют условию задачи и обращают это неравенство в верное равенство.

3.2. Да, обязательно.

Рассмотрим куб АВСDA'B'C'D' и какое-нибудь его шестиугольное сечение MNPQRT (рис. 7). Предположим, что диагонали RN, MQ и TP шестиугольника пересекаются в некоторой точке О.

Рис. 7

Способ I. Заметим, что прямая RN лежит в плоскости диагонального сечения BCD'A', а прямая MQ — в плоскости сечения ABC'D'. Следовательно, их общая точка О принадлежит BD' — прямой, по которой пересекаются указанные плоскости. Прямая TP лежит в плоскости сечения АСС'A', поэтому точка О должна являться точкой пересечения BD'и этой плоскости. Таким образом, О — центр куба.

Способ II. Противоположные стороны данного сечения попарно параллельны, так как принадлежат прямым пересечения плоскости сечения с противолежащими гранями куба. Следовательно, данное сечение разбивается диагоналями на три пары подобных треугольников: ∆МОN~∆QОR, ∆NОP~∆RОT, ∆PОQ~∆TОM. Тогда

Из равенства первого и последнего отношений получим, что MN=QR. Аналогично доказывается, что NP=RT и PQ=TM, то есть выписанные ранее пары треугольников не только подобны, но и равны. Тогда О — центр симметрии сечения.

Рассмотрим симметрию пространства с центром О. При этой симметрии образом точки М является точка Q, поэтому образом прямой АВ, проходящей через М, является ей параллельная прямая, проходящая через Q, то есть прямая С'D'. Аналогично доказывается, что и остальные прямые, содержащие ребра куба, попарно симметричны относительно О. Таким образом, при симметрии с центром О куб переходит в себя, значит, точка О — центр симметрии куба (точка пересечения диагоналей).

Комментарий. Отметим, что во втором способе решения попутно доказан следующий факт: если противолежащие стороны шестиугольника попарно параллельны, а диагонали пересекаются в одной точке, то эта точка – центр симметрии шестиугольника.

3.3. 198.

Пусть х — одно из искомых чисел, а у — сумма его цифр. По условию х = 11у, следовательно, х кратно 11.

Запишем полученное равенство по-другому: х – у = 10у. Так как числа х и у имеют одинаковые остатки при делении на 9, то число 10у кратно 9. Учитывая, что НОД(10; 9) = 1, получим, что у делится на 9, а значит, и х делится на 9. Таким образом, искомое число кратно 99.

Если десятичная запись числа х содержит n разрядов, то х≥10^{n – 1}, с другой стороны,

х = 11у ≤ 119n = 99n.

Следовательно, должно выполняться неравенство 10^{n – 1}≤99n. Это справедливо только для трех натуральных значений n: 1; 2 или 3.

Таким образом, х = 99р, где р равно 1, 2 или 3. У всех таких x сумма цифр равна 18, поэтому легко проверить, что решением задачи является только число 198.

4.1. Для положительных чисел а, b и c неравенство

равносильно неравенству

Поэтому достаточно доказать, что

Это неравенство равносильно неравенству:

(a + b + c)² ≥ 3ab + 3bc + 3ca
a² + b² + c² ≥ab + bc + ca.

Последнее неравенство выполняется для любых значений переменных, так как оно, в свою очередь, равносильно верному неравенству

(a – b)² + (b – c)² + (c – a)² ≥0.

4.2. R.

Способ I. Из прямоугольного треугольника CHK по теореме Пифагора получим: CK²=CH²+KH² (рис. 8). Высота CH прямоугольного треугольника ABC, проведенная к гипотенузе, является средним геометрическим проекций его катетов на гипотенузу, то есть CH²=AHBH.

Рис. 8

Через точку H проведем диаметр окружности PQ. Тогда, по теореме о произведении отрезков пересекающихся хорд окружности:

AHBH = PHQH = ( R – OH)(R + OH) = R² – OH².

Учитывая, что KН = ОН, получим:

CK² = AH×BH + OH² = R² – OH² + OH² = R².

Таким образом, CK = R.

Способ II. Пусть D — образ точки С при симметрии относительно прямой AB (рис. 9). Рассмотрим окружность w₁, описанную около треугольника ABC, и окружность w₂ с центром K и радиусом KC. Заметим, что точки C и D принадлежат обеим окружностям, то есть прямая CD является радикальной осью окружностей w₁ и w₂. Аналогично, прямая AB является радикальной осью данной окружности w и окружности w₁. Следовательно, общая точка H этих прямых является радикальным центром трех окружностей: w, w₁ и w₂, то есть H принадлежит общей хорде окружностей w и w₂. Так как H равноудалена от центров O и K данных окружностей, то радиусы окружностей равны, следовательно, CK = R.

Рис. 9

4.3. При n = 1 или n = 2.

При n = 1 оба данных числа являются простыми: nⁿ + 1 = 2 и (2n)²ⁿ + 1 = 5.

Пусть n > 1, тогда докажем, что n должно быть натуральной степенью числа 2. Пусть это не так, то есть n = 2^kp, где k — натуральное число или ноль, p — нечетное число, отличное от 1. Тогда

делится на и не равно этому числу, поэтому является составным.

Таким образом, n = 2^m, где m N. Тогда

Проведя рассуждения «от противного», аналогичные предыдущим (то есть предположив, что m или m + 1 имеют нечетный натуральный делитель, отличный от 1), получим, что рассматриваемые числа могут являться простыми только в том случае, когда оба числа m и m + 1 являются натуральными степенями числа 2.

Это возможно только при т = 1. Тогда оба данных числа действительно являются простыми:

nⁿ + 1 = 5 и (2n)²ⁿ + 1 = 257.

5.1. Да, существует.

Например, пусть тогда

так как для всех x [0; π] выполняется неравенство sin x ≥ 0.

5.2. 5 : 1.

Способ I. Пусть АВС — данный треугольник; AD, BE и CF — его высоты,

BH = HE = x, HF = y, CH = 2y

(рис. 10).

Так как ВЕС = ВFС = 90°, то точки B, F, E и С лежат на одной окружности, поэтому BHHE = CHHF. Тогда x² = 2y², то есть . Это означает, что треугольники BHF и CHE — прямоугольные равнобедренные, значит, CE = x; BF = y. Так как АВЕ = 45°, то АЕ = 2x, следовательно,

Прямоугольные треугольники ADC и АЕН подобны, поэтому

Следовательно,

Таким образом, значит,

Комментарий. Вычислив отношения, в которых точки Е и F делят стороны АС и АВ, можно было также воспользоваться теоремой Ван–Обеля, которая в данном случае записывается так:

Способ II. Эта задача является частным случаем классического утверждения элементарной геометрии, которое называется теоремой Жергонна: «Если Р — внутренняя точка треугольника АВС, а прямые АР, ВР и СР пересекают противолежащие стороны в точках А₁, В₁ и С₁ соответственно, то

»

(рис. 11).

Рис. 11

В нашем случае треугольник АВС — остроугольный, значит, ортоцентр Н — его внутренняя точка,

поэтому

тогда

Комментарий. Теорема Жергонна может быть доказана, например, так. Опустим перпендикуляры AA_h и PP_h на сторону ВС. Тогда

(теорема Фалеса или подобие прямоугольных треугольников). С другой стороны,

так как эти треугольники имеют общее основание ВС. Следовательно,

Выразив аналогичным образом два других отношения, получим:

Следовательно,

Ответ в задаче можно получить, не ссылаясь на теорему Жергонна. Достаточно провести рассуждения об отношении площадей из второй части доказательства теоремы.

Отметим, что теорема Жергонна обобщается для случая, когда точка Р лежит вне треугольника. Для этого вводится понятие отношения длин направленных отрезков. Тогда теорема Жергонна записывается в единой для всех случаев форме:

5.3. Мальчиков могло быть либо 9, либо 13.

Пусть на дискотеку пришли х мальчиков и у девочек. По условию х+у≤40. Рассмотрим произвольную пару, состоящую из мальчика и девочки. Если они знакомы, то в такой паре будет брошен взгляд девочки на мальчика, а если не знакомы, то будет брошен взгляд мальчика на девочку. То есть каждой паре соответствует ровно один взгляд. Общее количество таких пар (а значит, и взглядов) равно ху.

По условию ху = 117. Число 117 раскладывается на два натуральных множителя тремя способами: 117=1117 =339 =913. Так как сумма множителей должна быть не больше чем 40, то возможен только последний вариант. Значит, х = 9 или х = 13.

Блинков А., Блинков Ю., Френкин Б., Чулков П., Шноль Д.