Векторный метод решения стереометрических задач

Векторное решение многих стереометрических задач значительно проще их решения средствами элементарной геометрии («чисто геометрически»). Причина этого «упрощения» заключается в том, что при векторном методе решения можно обойтись без тех дополнительных построений, которые следует выполнять (аргументированно!) при «чисто геометрическом» решении даже простых задач.

Вместе с тем, чтобы векторы стали аппаратом решения геометрических задач, необходимо уметь переводить условие геометрической задачи в векторную терминологию и символику (на «векторный язык»), затем выполнять соответствующие алгебраические операции над векторами и, наконец, полученный в векторной форме результат переводить «обратно», на «геометрический язык».

Знание условия коллинеарности двух векторов и компланарности трех векторов позволяет в векторной форме решать аффинные задачи стереометрии — задачи, в которых изучаются вопросы взаимного расположения прямых и плоскостей. Свойства скалярного произведения двух векторов, условия перпендикулярности двух векторов позволяют легко перевести в векторную форму отношения перпендикулярности прямых и плоскостей и с помощью векторов решать метрические задачи — задачи, в которых находят расстояния, углы, площади, объемы геометрических фигур.

Одним словом, векторы — мощный аппарат решения стереометрических задач.

Линейные операции над векторами

Рабочими формулами при векторном способе решения аффинных задач стереометрии являются «формула : для середины М отрезка АВ и произвольной точки О пространства, а также «формула: для центроида М треугольника АВС и произвольной точки О пространства.

Задача 1. Отрезок, соединяющий вершину тетраэдра с центроидом противолежащей грани, называется медианой этого тетраэдра; отрезок, соединяющий середины противоположных ребер тетраэдра, называется его бимедианой. Докажите:

а) что все медианы тетраэдра пересекаются в одной точке и эта точка делит каждую из медиан в отношении 3:1, считая от вершины;

б) все бимедианы тетраэдра пересекаются в одной точке и делятся ею пополам;

в) точка пересечения бимедиан тетраэдра совпадает с точкой пересечения его медиан.

Решение.

а) Пусть Н₁, Н₂, Н₃, Н₄ — центроиды граней соответственно АВС, АВР, ВСР, АСР; М — точка, делящая медиану РН₁ тетраэдра РАВС в отношении РМ : МН₁ = 3 : 1( рис. 1).

Рис. 1

Тогда РМ : РН₁ = 3 : 4, откуда Для любой точки О пространства и центроида Н₁ грани АВС выполняется равенство:

Тогда

Аналогично можно доказать, что для точек М₁, М₂ и М₃, делящих медианы соответственно СН₂, АН₃, ВН₄ тетраэдра в отношении 3 : 1, считая соответственно от вершин С, А и В, выполняется то же равенство, то есть

Это означает, что точки М, М₁, М₂ и М₃ совпадают, то есть все четыре медианы РН₁, СН₂, АН₃ и ВН₄ тетраэдра пересекаются в одной точке М и делятся этой точкой в отношении 3 : 1, считая от соответствующей вершины, что и требовалось доказать.

Точка пересечения медиан тетраэдра называется центроидом этого тетраэдра.

б) Пусть точки K и Е — середины ребер соответственно ВС и АР (см. рис. 1), то есть отрезок KЕ — бимедиана тетраэдра РАВС. Если точка Q — середина бимедианы KЕ, то для любой точки О пространства выполняется:

Так как K и Е — середины ребер соответственно ВС и АР, то справедливы равенства:

Тогда получаем:

Аналогично можно доказать, что для середины Q₁ бимедианы ТF (см. рис.1) имеет место: Можно убедиться, что такое же равенство выполняется и для середины Q₂ третьей бимедианы данного тетраэдра. Это означает: откуда следует, что точки Q, Q₁ и Q₂ совпадают, то есть все три бимедианы тетраэдра пересекаются в одной точке Q и делятся этой точкой пополам.

в) Таким образом, для точек М и Q справедливы соответственно равенства:

и

из которых следует, что откуда: точка Q пересечения бимедиан тетраэдра РАВС совпадает с его центроидом М, что и требовалось доказать.

Условие компланарности трех векторов

В качестве базиса в пространстве можно выбрать любую упорядоченную тройку некомпланарных векторов Тогда любой вектор пространства единственным образом можно разложить по векторам этого базиса:

В общем виде критерий компланарности трех ненулевых векторов выражает равенство: (при условии, что не все коэффициенты одновременно равны нулю). Если в задаче требуется доказать, что три данные прямые параллельны некоторой плоскости (ее положение определять не нужно), то достаточно на каждой из этих прямых выбрать вектор и, используя признак компланарности трех векторов, доказать, что выбранные векторы компланарны.

Задача 2.В параллелепипеде АВСDА₁В₁С₁D₁ точка М — середина диагонали А₁С₁ грани A₁B₁C₁D₁, точка K — середина ребра ВВ₁. Докажите, что прямые А₁В₁, KМ и ВС₁ параллельны некоторой плоскости.

Рис. 2

Решение. Введем векторы: (рис.2).

Тройку некомпланарных векторов примем в качестве базиса. Разложим векторы по векторам этого базиса.

Имеем:

Тогда

Это означает, что векторы компланарны, следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А₁В₁, KМ и ВС₁, для которых векторы являются направляющими.

Задача 3. На диагоналях АВ₁ и ВС₁ граней AA₁B₁B и ВВ₁С₁С параллелепипеда ABCDA₁B₁C₁D₁ взяты точки соответственно Н и M так, что отрезки MН и A₁C параллельны. Найдите отношение длин этих отрезков.

Решение. Введем векторы: (рис.3).

Рис. 3

Тройку некомпланарных векторов примем в качестве базиса и разложим векторы по векторам этого базиса. Имеем:

Так как точка Н лежит на диагонали АВ₁, то векторы коллинеарны, поэтому существует такое число х, что Аналогично, в силу коллинеарности векторов существует такое число у, что

По правилу ломаной находим:

По условию MН A₁C, значит, существует такое число t, что то есть выполняется равенство:

Вследствие некомпланарности векторов и единственности разложения вектора по базису, приходим к выводу: 1 – х – t = 0, t – у = 0, х – у – t = 0. Решением этой системы уравнений является: Тогда значит, МН : СА₁ = 1 : 3.

Ответ: 1 : 3.

Скалярное произведение двух векторов

С помощью скалярного произведения двух векторов можно находить длину отрезка, величину угла, следовательно, находить расстояния, площади и другие метрические характеристики геометрических фигур. Для доказательства перпендикулярности прямых и плоскостей удобно пользоваться признаком перпендикулярности двух ненулевых векторов:

Для нахождения длины отрезка АВ векторным способом в качестве базисных выбирают такие векторы, длины которых и углы между которыми уже известны. Затем записывают разложение вектора по базисным векторам и находят:

Если в задаче требуется найти величину угла j, то в качестве базисных принимают векторы с известными отношениями их длин и углами между ними. Затем выбирают векторы на сторонах этого угла с началом в его вершине и разлагают их по базису, после чего находят cos φ по формуле

Задача 4. В кубе ABCDA₁B₁C₁D₁, ребро которого равно 6, найдите:

а) расстояние от вершины А₁ до плоскости ВС₁D;

б) угол между диагональю ВА₁ грани АА₁В₁В и плоскостью ВС₁D .

Решение. а) Пусть отрезок A₁М — перпендикуляр из вершины А₁ на (ВС₁D), М(ВС₁D) (рис. 4). Тогда A₁М = ρ(А₁; (ВС₁D)). Найдем длину отрезка A₁М.

Рис. 4

По правилу треугольника имеем:

Обозначим: а в плоскости ВС₁D введем базис где и запишем разложение вектора по векторам этого базиса в виде: Тогда

Так как A₁М(ВС₁D), то A₁МВС₁, A₁МВD (по определению прямой, перпендикулярной плоскости), значит,

Коэффициенты х и у в разложении вектора найдем, пользуясь условием:

которое равносильно системе уравнений

          (*)

Прежде чем решать эту систему уравнений, найдем скалярные произведения векторов:

Так как треугольники ВС₁D, A₁ВС₁, A₁ВDv— правильные и равные, то длины их сторон равны а

Тогда:

          (**)

          (***)

Вернемся к решению системы уравнений (*).

Учитывая соотношения (**) и (***) и свойства скалярного произведения векторов, получаем:

Тогда и

Таким образом,

б) Обозначим (ВА₁; (ВС₁D)) = φ. Так как А₁М (ВС₁D), то ВМ — ортогональная проекция ВС₁ на (ВС₁D),

значит, (ВА₁; (ВС₁D)) = (ВА₁; ВМ)= = А₁ВМ = φ.

Используя соотношения (**) и (***) и то, что вектор при имеет вид находим:

Ответ:

Задача 5. Найдите расстояние между скрещивающимися диагоналями АВ₁ и ВС₁ смежных граней АА₁В₁В и ВВ₁С₁С куба ABCDA₁B₁C₁D₁, если ребро этого куба равно 12.

Решение. Введем векторы: (рис.5). Тройку некомпланарных векторов примем в качестве базиса и разложим векторы по векторам этого базиса. Имеем:

Рис. 5

Пусть отрезок МН — общий перпендикуляр прямых АВ₁ и ВС₁ (НАВ₁, МВС₁). Тогда длина отрезка МН равна расстоянию между этими прямыми:ρ(АВ₁; ВС₁) = | МН |.

Так как точка Н лежит на диагонали АВ₁, то векторы коллинеарны, поэтому существует такое число х, что

Аналогично, в силу коллинеарности векторов существует такое число у, что

По правилу ломаной находим:

Значения х и у найдем из условия:

           (1)

Учитывая, что базисные векторы попарно взаимно перпендикулярны и длина каждого из них равна 12, имеем:

Получаем:

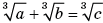
Таким образом, система векторных равенств (1) равносильна системе уравнений решением которой является:

Тогда

Значит,

Ответ:

Многогранники, фигуры вращения и векторы

Задача 6. Около правильной четырехугольной пирамиды, каждое ребро которой равно 10, описан цилиндр так, что все вершины пирамиды находятся на окружностях оснований цилиндра. Найдите объем и площадь боковой поверхности цилиндра.

Решение. Пусть вершина Р данной пирамиды РАВСD лежит на окружности с центром О нижнего основания цилиндра, описанного около этой пирамиды (рис.6).

Так как каждое ребро пирамиды равно 10, то радиус R окружности основания, описанной около правильного треугольника РАВ со стороной 10, равен

Пусть точка М — середина ребра СD, МK — перпендикуляр из М на плоскость АВС основания цилиндра, K(АВС). Тогда МK ВА, МK ВР (по определению прямой, перпендикулярной плоскости), при этом высота h цилиндра равна .

Рис. 6

Найдем для этого введем в качестве базисных некомпланарные векторы разложим вектор в базисе и найдем

Имеем:

Тогда

Значения х и у найдем из условия:

           (2)

Система (2) равносильна системе уравнений

            (3)

Прежде чем решать эту систему уравнений, найдем скалярные произведения векторов:

Имеем: треугольники АВР, РВС — правильные и равные, а длины их сторон равны АВСD — квадрат со стороной 10, поэтому

Тогда:

           (4)

           (5)

           (6)

Продолжим решение системы уравнений (3). На основании свойств скалярного произведения векторов, учитывая (4)–(6), получаем:

Тогда:

и

Значит,

Ответ:

Сфера, описанная около тетраэдра, и векторы

Если даны длины трех ребер РА, РВ и РС тетраэдра РАВС, исходящих из его вершины Р, а также известны величины плоских углов при этой вершине, то с помощью векторов можно найти радиус, а следовательно и площадь сферы (объем шара), описанной (описанного) около этого тетраэдра.

Рассмотрим следующие задачи.

Задача 7. В треугольной пирамиде РАВС все плоские углы при вершине Р прямые. Найдите площадь сферы, описанной около этой пирамиды, если РА = 2, РВ = 3, РС = 4.

Решение. Пусть точка О — центр сферы, описанной около тетраэдра РАВС, R — радиус этой сферы. Тогда ОА = ОВ = ОС = ОР = R.

Введем некомпланарные векторы (рис.7) и примем их в качестве базисных в пространстве. Тогда при этом Найдем коэффициенты х, у и z в этом разложении вектора

Рис. 7

По правилу треугольника имеем:

откуда

Из равенств ОА = ОВ = ОС = ОР (как радиусы сферы, описанной около тетраэдра РАВС) следует, что значит,

Тогда получаем:

Заметим, что так как базисные векторы попарно перпендикулярны и длины их равны соответственно 2, 3 и 4, то

           (7)

Заменяя выражением в последней системе уравнений и учитывая (7), получаем:

Тогда

и

Значит,

Ответ: 29π.

Аналогично векторным методом можно решить следующие задачи.

Задача 8. В тетраэдре РАВС два плоских угла при вершине Р прямые, а величина третьего плоского угла равна 60°. Найдите радиус сферы, описанной около этой пирамиды, если РА = РВ= РС = 12.

Ответ: . Указание. См. задачу 6. В качестве базисных принять векторы

Задача 9. В тетраэдре РАВС все плоские углы при вершине Р прямые. Найдите радиус сферы, описанной около этой пирамиды, если РА = РВ= РС = 6.

Ответ: . Указание. См. задачу 6. В качестве базисных принять векторы

Трехгранный угол, сфера и векторы

Если известны величины плоских углов при вершине Р трехгранного угла РАВС и дано расстояние РО от этой вершины до центра О сферы, касающейся всех трех ребер РА, РВ и РС этого угла, то можно найти радиус, а значит и площадь этой сферы.

Рассмотрим следующие задачи.

Задача 10. В трехгранном угле РАВС известны величины плоских углов при вершине Р:

АРВ = ВРС = АРС = 60°.

Сфера, центр которой удален от вершины Р на расстояние, равное касается всех ребер этого угла. Найдите радиус данной сферы.

Решение. Пусть сфера касается ребер РА, РВ и РС в точках соответственно K, Н и М. Тогда РK = РН = РМ (как отрезки касательных, проведенных к сфере из точки Р), при этом ОK = ОН = ОМ = R (R — радиус сферы), ОK РА, ОН РВ, ОМ РС (как радиусы сферы, проведенные в точки касания ее с ребрами угла).

Введем некомпланарные векторы (рис. 8) и примем их в качестве базисных в пространстве. Тогда причем

Рис. 8

Так как РK = РН = РМ, то

Найдем значения коэффициентов х, у, z разложения вектора используя следующий факт: ОK РА, ОН РВ, ОМ РС, то есть Имеем:

При этом:

Заменив в трех последних равенствах вектор выражением получаем:

Найдем скалярные произведения векторов:

Имеем:

АРВ = ВРС = АРС = 60°;

Тогда:

	(9)            (10)

Продолжим решение системы уравнений (8).

После деления на m² обеих частей каждого уравнения системы (8), учитывая (9)–(10), получаем:

После сложения всех уравнений последней системы получаем: х + у + z = 1,5. Тогда из первого уравнения 2х + у + z = 2 получаем: х + 1,5 = 2, откуда х = 0,5. Аналогично, из второго и третьего уравнений системы находим: у = 0,5, z = 0,5.

Таким образом,

(Равенство коэффициентов разложения вектора означает, что центр О сферы, касающейся всех ребер трехгранного угла с плоскими углами в 60°, лежит на прямой пересечения биссектральных плоскостей двугранных углов при ребрах этого трехгранного угла.)

Найдем длины базисных векторов и учитывая условие и соотношения (9)–(10).

Получаем:

Тогда имеем:

Теперь найдем радиус R сферы, учитывая, что

Имеем:

Тогда

Ответ:

Аналогично векторным методом можно решить следующие задачи.

Задача 11. В трехгранном угле РАВС известны величины плоских углов при вершине Р:
АРВ = ВРС = АРС = 90°. Сфера, центр которой удален от вершины Р на расстояние касается всех ребер этого угла. Найдите радиус данной сферы.

Ответ: Указание. Если сфера касается ребер РА, РВ и РС в точках соответственно K, Н и М, то в качестве базисных принять векторы

Ответ: Указание. Если сфера касается ребер РА, РВ и РС в точках соответственно K, Н и М, то в качестве базисных принять векторы

Задачи, аналогичные разобранным в тексте данной статьи, можно найти в задачниках для 10-го и 11-го классов авторов Л.Звавич, Е.Потоскуев: в задачнике 10-го задачи: 6.018, 6.030, 6.044–6.047, 6.067, 6.089, 6.090, 6.106–6.110, 6.114, 6.115, 6.120-6.125; в задачнике 11-го задачи: 2.101, 2.102, 2.351–2.354, 2.394, 3.040, 3.216, 3.217, 3.228, 3.229, 3.285–3.287.

Потоскуев Е.