Уравнения вида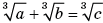

1. Введение

Уравнения вида

      (1)

где a, b, c — некоторые функции от одной неизвестной x, регулярно предлагаются на вступительных экзаменах в высшие учебные заведения. В общем виде, когда нет никаких «хороших» связей между выражениями a, b, c, даже избавиться от кубических радикалов простым последовательным возведением обеих частей уравнения в третью степень нельзя. Для этого нужно применять одно нестандартное преобразование (ниже мы его опишем). Каким бы сложным ни казалось это преобразование, вопрос о его равносильности еще сложнее. В настоящей статье мы опишем как процедуру, позволяющую в общем случае избавиться от радикалов в уравнении (1), так и выясним необходимые и достаточные условия для ее равносильности.

2. Избавление от иррациональности

Начинать решение уравнения (1), конечно, естественно с почленного возведения в куб:

      (2)

Применяя тождества

мы получим:

      (3)

Чтобы избавиться от оставшихся кубических радикалов, необходимо еще одно возведение в куб. Перед этой операцией, в соответствии с общей идеологией решения иррациональных уравнений, необходимо изолировать радикалы:

      (4)

Левая часть этого уравнения имеет тот же вид, что и левая часть исходного уравнения (1); она является суммой двух кубических радикалов. Поэтому повторное возведение в третью степень опять требует применения тождества (x + y)³ = x³ + 3x²y + 3xy² + y³, что приведет к возобновлению иррациональностей в членах вида 3x²y и 3xy².

Обойти эту проблему можно, если в левой части уравнения (4) вынести за скобку произведение

      (5)

а затем вспомнить исходное уравнение (1) и заменить сумму

      (6)

В уравнении (6) возведение в куб уже позволяет избавиться от радикалов:

27abc = (c – a – b)³.       (7)

Центральную роль в проведенных рассуждениях играет переход от уравнения (5) к уравнению (6). Он интересен тем, что в отличие от «обычных» преобразований, которые базируются только на последнем полученном уравнении-следствии, подключаются и предыдущие уравнения. Этот переход подключает нашу «память», и мы используем его для выполнения ранее полученные выводы. Хотя в математике (например, в геометрии) это обычная манера рассуждений, в алгебре, которая школьниками обычно воспринимается как написание цепочки равенств, заканчивающейся линейным или квадратным уравнением, эта идея довольно необычна.

При решении конкретных уравнения описанная общая схема обычно упрощается. Например, в выражении c – a – b часто удается привести подобные члены. Поэтому уравнение (7) обычно довольно простое целое или дробно-рациональное уравнение, которое решается без труда.

Однако это не означает, что исходное уравнение решено. Дело в том, что хотя переходы

• от уравнения (1) к уравнению (2),
• от уравнения (2) к уравнению (3),
• от уравнения (3) к уравнению (4),
• от уравнения (4) к уравнению (5),
• от уравнения (6) к уравнению (7),

очевидно, равносильны, центральный переход от уравнения (5) к уравнению (6), вообще говоря, не является равносильным преобразованием и поэтому будет нужна серьезная проверка.

Если корни последнего уравнения-следствия (7) являются «красивыми» числами, например, т.п, эта проверка не вызывает никаких затруднений. В противном случае проверка превращается в сложную техническую задачу, может быть, даже более сложную, чем получение и решение последнего уравнения-следствия.

3. Равносильность

Выясним теперь, при каких условиях преобразование (5) Þ (6) является равносильным, то есть когда уравнение (6) влечет уравнение (5). Поскольку уравнение (5) равносильно исходному уравнению (1), можно анализировать условия, при которых уравнение (6) влечет уравнение (1).

Обозначим для сокращения записей через A, B, C соответственно. Тогда уравнение (6) примет вид:

3ABC = C³ – A³ – B³.

Его можно рассматривать как кубическое уравнение относительно C:

C³ – 3AB∙C – (A³ + B³) = 0.       (8)

Нетрудно проверить, что C₀ = A + B будет корнем этого уравнения. Поэтому многочлен C³ – 3AB∙C – (A³ + B³) можно разложить на множители, причем одним из множителей будет C – C₀ C – (A + B). Второй множитель можно найти делением многочлена C³ – 3AB∙C – (A³ + B³) на двучлен C – (A + B); он равен C² + (A + B)C + (A² – AB + B²).

Следовательно, уравнение (8) распадается на два уравнения:

C – (A + B) = 0;

C² + (A + B)C + (A² – AB + B²) = 0.

В терминах переменных a, b, c первое уравнение — это в точности уравнение (1).

Уравнение

C² + (A + B)C + (A² – AB + B²) = 0       (9)

является квадратным (относительно C). Его дискриминант равен

D = (A + B)² – 4(A² – AB + B²) = –3(A – B)² ≤ 0.

Если уравнение (9) имеет решение, то его дискриминант должен быть равен нулю, то есть A = B.
Тогда

Итак, уравнение (9) равносильно системе

Для запоминания удобна следующая форма этой системы:

Если решения этой системы удовлетворяют исходному уравнению (1), то эти решения не являются «лишними» корнями уравнения. В связи с этим последнюю систему удобно разбить на две системы:

«Лишние» корни уравнения (6) и только они являются решениями второй из этих систем. С учетом равенств a = –c, b = –c условие можно записать в виде c ≠ 0.

Если система

несовместна, то анализируемое преобразование — равносильно. В противном случае множество ее решений — это все «лишние» корни уравнения (6).

4. Примеры решения уравнений

Задача 1. (Географический факультет МГУ, 1995, май, задача № 5.) Решить уравнение       (11)

Решение. Способ I. Чтобы избавиться от радикалов, применим описанную выше общую процедуру, но перед этим перенесем член в правую часть (это немного упростит выкладки):

Теперь вспомним исходное уравнение (12) и заменим

      (14)

В уравнении (14) возведение в куб позволяет избавиться от радикалов:

(x – 1)³ = –4x(x – 1) x – 1 = 0 x = 1;

(x – 1)³ = –4x(x – 1) x² – 2x + 1 = –4x

x² + 2x + 1 = 0 x = –1.

Как мы отмечали, переход от уравнения (13) к уравнению (14), вообще говоря, не является равносильным преобразованием и поэтому нужна проверка.

Подстановка на место неизвестной числа x = 1 дает числовое равенство 1 + 0 = 1, которое истинно, так что x = 1 является корнем данного уравнения.

Подстановка на место неизвестной числа x = –1 дает числовое равенство –1 – 1 = 1, которое ложно, так что x = –1 не является корнем исходного уравнения.

Посмотрим теперь, что для уравнения (12) дает теория, развитая нами в разделе 3. Система (10) примет вид:

Она имеет единственное решение x = –1. Поэтому из найденных корней уравнения (14), x₁ = 1 и x₂ = –1, корень x₂ = –1 является «лишним», а корень x₁ = 1 удовлетворяет исходному уравнению (12).

Способ II. Описанная в разделе 2 общая схема решения уравнений вида может быть заменена более простыми преобразованиями, если выражения a, b, c обладают «хорошими» свойствами. Для уравнения (12) таким «хорошим» свойством является наличие под радикалами линейных выражений. Поэтому от одного радикала можно избавиться, обозначив его новой буквой. Пусть, например, Тогда x = t³ и уравнение (11) примет вид:

Изолируя радикал и возводя его в куб, получим:

(t – 1)(t² + t + 1) + 2(t – 1)³ = 0

3(t – 1)(t² – t + 1) = 0 t = 1

(так как дискриминант квадратного трехчлена t² – t + 1 отрицателен, вторая скобка не может быть равна нулю).

Значит, исходное уравнение равносильно уравнению которое имеет единственный корень x = 1.

Способ III. Отметим, что описанные выше методы решения, строго говоря, не решают исходное уравнение с кубическими радикалами, а лишь упрощают его до уравнения без радикалов. При этом нельзя исключить, что последнее уравнение окажется сложнее исходного иррационального уравнения. С другой стороны, в ряде случаев исходное иррациональное уравнение можно решить и не убирая радикалы. Мы продемонстрируем это на примере уравнения (11).

Рассмотрим левую часть уравнения (11) как функцию от переменной x:

Эта функция является суммой двух функций,

Каждая из этих функций монотонно возрастает от –∞ до +∞ (как суперпозиция функций и линейной функции z = x или соответственно). Поэтому и функция f(x) монотонно возрастает от –∞до +∞. Графиком правой части исходного уравнения является горизонтальная прямая y = 1. Из этих свойств левой и правой частей исходного уравнения следует, что оно имеет ровно один корень x₀. Сам корень можно находить любым способом, например, последовательно подставляя различные числа. Поскольку f(x₀) должно быть равно 1, начать следует с чисел, для которых «извлекаются» кубические корни и Первое такое число — это x = 1. Оно и будет искомым корнем.

Если бы попытка была безуспешной, она, тем не менее, давала бы важную информацию о положении искомого корня на числовой оси и тем самым облегчала бы последующие попытки. Если бы мы начали, например, с числа 0, то мы бы получили, что что, тем более, ниже уровня y = 1. Поэтому искомый корень x₀ > 0. Если бы мы взяли в качестве следующего числа x = 2, то мы бы получили, что Поэтому x₀ < 2.

Ответ: 1.

Прием с введением новой неизвестной, который мы использовали во втором способе решения задачи 1, успешно работает при решении многих других уравнений вида (конечно, при наличии определенных «хороших» связей между выражениями a, b, c).

Задача 2.  (Социологический факультет МГУ, 2001, июль, задача № 6.) Решить уравнение       (15)

Решение. Способ I. Запишем дроби и стоящие под знаками радикалов, как соответственно:

Наличие повторяющихся блоков позволяет ввести новую неизвестную Для нее исходное уравнение примет вид:

Как и в уравнении (12), в полученном уравнении под радикалами стоят линейные выражения. Поэтому от одного радикала можно избавиться, обозначив его новой буквой. Пусть, например, Тогда t = u³ – 1 и уравнение примет вид:

Изолируя радикал и возводя в куб, получим:

u³ – 7 = (u – 1)³

u² – u – 2 = 0

u₁ = –1, u₂ = 2.

Соответственно, для неизвестной t = u³ – 1 мы имеем два значения: t₁ = –2 и t₂ = 7. Возвращаясь к основной неизвестной мы также получим два значения:

Поскольку все проделанные преобразования равносильны (мы лишь возводили в куб, переносили члены из одной части в другую, вводили новые неизвестные и т.п.), проверка не нужна.

Специфика уравнения (15) позволяет предложить еще один простой метод его решения, основанный на введении новой неизвестной и потому не требующий проверки.

Способ II. Перенесем член из левой части уравнения (15) в правую:

и возведем обе части полученного уравнения в куб:

Изолируя радикалы, мы получим:

Поскольку в этом уравнении повторяется блок введем новую неизвестную Для нее последнее уравнение примет вид: y² + y – 2 = 0.

Это квадратное уравнение имеет два корня: y₁ = 1, y₂ = –2. Возвращаясь к основной неизвестной x, мы получим два уравнения:

Конечно, наряду с двумя описанными выше методами решения уравнения (15), которые эксплуатировали особенности подкоренных выражений, работает и общий метод, описанный в разделе 2.

Ответ:

Задача 3. (Факультет вычислительной математики и кибернетики МГУ, устный экзамен, 2000, 2005.) Решить уравнение       (16)

Решение. Начиная, как обычно, с почленного возведения в куб, мы получим:

Теперь заменим и изолируем радикалы:

      (17)

При этом, имея в виду, что после очередного возведения в куб получится алгебраическое уравнение высокой степени, которое, видимо, нужно будет решать разложением на множители более низкой степени, мы разложили правую часть на множители.

Теперь возводим уравнение (17) в куб:

54x³(x – 1)(x + 1) = 8x³(x – 1)³(x + 1)³

27x³(x – 1)(x + 1) – 4x³(x – 1)³(x + 1)³ = 0

x³(x – 1)(x + 1)(27 – 4(x – 1)²(x + 1)²) = 0.

Последнее уравнение (9-й степени) распадается на четыре уравнения:

• три простейших линейных уравнения x = 0, x – 1 = 0, x + 1 = 0, корни которых — числа 0, 2, –1 соответственно,
• уравнение четвертой степени

27 – 4(x – 1)²(x + 1)² = 0.       (18)

Уравнение (18) заменой t = x² – 1 сводится к неполному квадратному уравнению 27 – 4t² = 0. Это уравнение имеет два корня

Возвращаясь к основной неизвестной x, мы получим два квадратных уравнения:

Поскольку первое из них не имеет корней. Второе уравнение имеет два корня:

Итак, применение для решения уравнения (16) общего алгоритма, описанного в разделе 2, дало пять чисел, которые могут претендовать на роль его корней:

Прямая проверка (простой подстановкой в исходное уравнение) без труда может быть выполнена для чисел 0, 1, –1 (она показывает, что все три числа являются корнями исходного уравнения). Попытка же прямой проверки чисел приведет к настолько громоздкому числовому равенству, что выяснение его истинности или ложности — это самостоятельная очень сложная задача на упрощение иррациональных числовых выражений.

Посмотрим теперь, что для уравнения (16) дает теория, развитая нами в разделе 3. Система (10) пример вид:

Два первых уравнения этой системы влекут, что x – 1 = x + 1, то есть –1 = 1. Поэтому система (19) несовместна, так что «лишних» корней нет.

Ответ:

Задачи для самостоятельного решения

4. (Социологический факультет МГУ, 2001, июль, задача № 6.) Решите уравнение

5. (Факультет вычислительной математики и кибернетики МГУ, устный экзамен, 2003.) Решите уравнение

6. (Механико-математический факультет МГУ, 2000, заочный тур олимпиады «Абитуриент-2000», задача № 2.) Решите уравнение

Ответ: 4.   5. –3; 4.  6. {0; 2; 13; 15}.

Фалин А., Фалин Г.