Решаем задачи по геометрии: пропорциональные отрезки

Теорема 1 (теорема Фалеса). Параллельные прямые высекают на пересекающих их прямых пропорциональные отрезки (рис. 1).

Определение 1. Два треугольника (рис. 2) называются подобными, если соответствующие стороны у них пропорциональны.

Теорема 2 (первый признак подобия). Если угол первого треугольника равен углу второго треугольника, а прилежащие к этим углам стороны треугольников пропорциональны, то такие треугольники подобны (см. рис. 2).

Теорема 3 (второй признак подобия). Если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис. 3).

Теорема 4 (теорема Менелая). Если некоторая прямая пересекает стороны AB и BC треугольника ABC в точках X и Y соответственно, а продолжение стороны AC — в точке Z (рис. 4), то

Теорема 5. Пусть в остроугольном треугольнике ABC проведены высоты AA1 и CC1 (рис. 5). Тогда треугольники A1BC1 и ABC подобны, причем коэффициент подобия равен cos ∠B.

Лемма 1. Если стороны AC и DF треугольников ABC и DEF лежат на одной прямой или на параллельных прямых (рис. 6), то

Лемма 2. Если два треугольника имеют общую сторону AC (рис. 7), то

Лемма 3. Если треугольники ABC и AB1C1 имеют общий угол A, то

Лемма 4. Площади подобных треугольников относятся как квадрат коэффициента подобия.

Доказательства некоторых теорем

Доказательство теоремы 4. Проведем через точку C прямую, параллельную прямой AB, до пересечения с прямой XZ в точке K (рис. 9). Надо доказать, что

Рассмотрим две пары подобных треугольников:

Перемножив почленно эти равенства, получим:

что и требовалось доказать.

Доказательство теоремы 5. Докажем подобие треугольников A1BC1 и ABC при помощи первого признака подобия. Так как эти два треугольника имеют общий угол B, достаточно доказать, что

Но это следует из того, что из прямоугольного треугольника ABA1, а из прямоугольного треугольника CBC1. Попутно доказана и вторая часть теоремы.

Решения задач

Задача 1. Дана трапеция ABCD, причем известно, что BC = a и AD = b. Параллельно ее основаниям BC и AD проведена прямая, пересекающая сторону AB в точке P, диагональ AC в точке L, диагональ BD в точке R и сторону CD в точке Q (рис. 10). Известно, что PL = LR. Найти PQ.

Решение. Докажем сначала, что PL = RQ. Рассмотрим две пары подобных треугольников:

Согласно теореме Фалеса имеем:

Обозначим теперь PL = LR = RQ = x и рассмотрим снова две пары подобных треугольников:

Имеем далее:

Значит,
Ответ:

Задача 2. В треугольнике ABC угол A равен 45°, а угол C — острый. Из середины N стороны BC опущен перпендикуляр NM на сторону AC (рис. 11). Площади треугольников NMC и ABC относятся соответственно как 1 : 8. Найти углы треугольника ABC.

Решение. Пусть BH — высота, опущенная из вершины B на сторону AC.
Так как NM — средняя линия треугольника BHC, то S∆BHC = 4S∆NMC.
Но, согласно условию задачи, S∆ABC = 8S∆NMC.
Следовательно, S∆ABC = 2S∆BHC, поэтому S∆ABH = S∆BHC. Значит, AH = HC,
откуда ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Ответ: ∠CAB = ∠ACB = 45°, ∠ABC = 90°.

Задача 3. Дан треугольник ABC, в котором угол B равен 30°, AB = 4 и BC = 6. Биссектриса угла B пересекает сторону AC в точке D (рис. 12). Определить площадь треугольника ABD.

Решение. Применим к треугольнику ABC теорему о биссектрисе внутреннего угла:

Значит,

Ответ:

Задача 4. Через середину M стороны BC параллелограмма ABCD, площадь которого равна 1, и вершину A проведена прямая, пересекающая диагональ BD в точке O (рис. 13). Найти площадь четырехугольника OMCD.
Решение. Площадь четырехугольника OMCD будем искать как разность площадей треугольников BCD и BOM. Площадь треугольника BCD равна половине площади параллелограмма ABCD и равна Найдем площадь треугольника BOM. Имеем:

∆BOM ∼ ∆AOD ⇒
Далее:

Значит,

Ответ:

Задача 5. В прямоугольный равнобедренный треугольник ABC с прямым углом при вершине B вписан прямоугольный треугольник MNC так, что угол MNC прямой, точка N лежит на AC, а точка M на стороне AB (рис. 14). В каком отношении точка N должна делить гипотенузу AC, чтобы площадь треугольника MNC составляла от площади треугольника ABC?

Решение. Можно считать, что AB = 1. Обозначим AM = x, 0 < x < 1, тогда BM = 1 – x,

Имеем:

Ответ: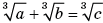

Задача 6. В трапеции ABCD диагональ AC перпендикулярна боковой стороне CD, а диагональ DB перпендикулярна боковой стороне AB. Продолжения боковых сторон AB и DC пересекаются в точке K, образуя треугольник AKD с углом 45° при вершине K (рис. 15). Площадь трапеции ABCD равна S. Найти площадь треугольника AKD.

Решение. Согласно теореме 5, треугольник BKC подобен треугольнику AKD с коэффициентом подобия Следовательно, площади этих треугольников относятся как 1 : 2, а это значит, что площадь трапеции ABCD равна площади треугольника BKC. Поэтому площадь треугольника AKD равна 2S.
Ответ: 2S.

Задача 7. В треугольнике ABC на стороне AB взята точка K так, что AK : KB = 1 : 2, а на стороне BC взята точка L так, что CL : LB = 2 : 1. Пусть Q — точка пересечения прямых AL и CK (рис. 16). Найти площадь треугольника ABC, зная, что площадь треугольника BQC равна 1.

Решение. Пусть AK = x, BL = y. Тогда KB = 2x,
LC = 2y, значит, AB = 3x и BC = 3y. Применим к треугольнику ABL и секущей KQ теорему Менелая:

Далее применим к треугольникам ABC и QBC лемму о площадях, получим:

Ответ:

Задача 8. Из точки M, которая расположена внутри остроугольного треугольника ABC, опущены перпендикуляры на стороны (рис. 17). Длины сторон и опущенных на них перпендикуляров соответственно равны a и k, b и m, c и n. Вычислить отношение площади треугольника ABC к площади треугольника, вершинами которого служат основания перпендикуляров.

Решение. Введем стандартные обозначения, то есть обозначим длины сторон треугольника ABC: BC = a, CA = b, AB = c; величины углов: ∠BAC = α,
∠ABC = β, ∠ACB = γ. Основания перпендикуляров, опущенных из точки M на стороны BC, CA и AB, обозначим соответственно через D, E и F. Тогда, согласно условию задачи, MD = k, ME = m, MF = n. Очевидно, что угол EMF равен π – α, угол DMF равен π – β, угол DME равен π – γ и точка M расположена внутри треугольника DEF. Площадь треугольника DEF равна:

Площадь треугольника ABC равна:

Найдем отношение площадей треугольников DEF и ABC:

Следовательно,

Ответ:

Задача 9. Точки P и Q расположены на стороне BC треугольника ABC так, что BP : PQ : QC = 1 : 2 : 3.
Точка R делит сторону AC этого треугольника таким образом, что AR : RC = 1 : 2 (рис. 18). Чему равно отношение площади четырехугольника PQST к площади треугольника ABC, где S и T — точки пересечения прямой BR с прямыми AQ и AP соответственно?

Решение. Обозначим BP = x, AR = y; тогда
PQ = 2x, QC = 3x, RC = 2y. Вычислим, какую часть площадь четырехугольника PQST составляет от площади треугольника APQ, а значит, и от площади треугольника ABC. Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая:

Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR, получим:

Далее:

С другой стороны, применив лемму о площадях к треугольникам APQ и ABC, получим, что

Ответ:

Задача 10. В треугольнике ABC длина высоты BD равна 6, длина медианы CE равна 5, расстояние от точки пересечения BD с CE до стороны AC равно 1 (рис. 19). Найти длину стороны AB.

Решение. Пусть точка O — точка пересечения прямых BD и CE. Расстояние от точки O до стороны AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая:

Применив теперь теорему Менелая к треугольнику ACE и секущей OD, получим, что

откуда OE = 2CO, и с учетом OE + CO = CE = 5
получаем, что К прямоугольному треугольнику CDO применим теорему Пифагора:

Значит, Наконец, рассмотрим прямоугольный треугольник ABD, в нем также воспользуемся теоремой Пифагора:

Ответ:

Задача 11. На отрезке AB лежат точки C и D, причем точка C находится между точками A и D. Точка M взята так, что прямые AM и MD перпендикулярны, и прямые CM и MB тоже перпендикулярны (рис. 20). Найти площадь треугольника AMB, если известно, что величина угла CMD равна α, а площади треугольников AMD и CMB равны S1 и S2 соответственно.

Решение. Обозначим площади треугольников AMB и CMD соответственно через
x и y (x > y). Заметим, что x + y = S1 + S2. Покажем теперь, что xy = S₁S₂sin² α. Действительно,

Аналогично,

так как ∠AMB = ∠AMC + ∠CMD + ∠DMB =
= 90° – α + α + 90° – α = 180° – α, и sin ∠AMB =
= sin α. Значит:

Таким образом, числа x и y являются корнями квадратного уравнения
t2 – (S1 + S2)t + S1S2sin2 α = 0.
Больший корень этого уравнения:

Ответ:

Задачи для самостоятельного решения

С-1. В треугольнике ABC, площадь которого равна S, проведена биссектриса CE и медиана BD, пересекающиеся в точке O. Найдите площадь четырехугольника ADOE, зная, что BC = a, AC = b.
С-2. В равнобедренный треугольник ABC вписан квадрат так, что две его вершины лежат на основании BC, а две другие — на боковых сторонах треугольника. Сторона квадрата относится к радиусу круга, вписанного в треугольник, как
8 : 5. Найдите углы треугольника.
С-3. В параллелограмме ABCD со сторонами AD = 5 и AB = 4 проведен отрезок EF, соединяющий точку E стороны BC с точкой F стороны CD. Точки E и F выбраны так, что
BE : EC = 1 : 2, CF : FE = 1 : 5. Известно, что точка M пересечения диагонали AC с отрезком FE удовлетворяет условию MF : ME = 1 : 4. Найдите диагонали параллелограмма.
С-4. Площадь трапеции ABCD равна 6. Пусть E — точка пересечения продолжений боковых сторон этой трапеции. Через точку E и точку пересечения диагоналей трапеции проведена прямая, которая пересекает меньшее основание BC в точке P, большее основание AD — в точке Q. Точка F лежит на отрезке EC, причем EF : FC = EP : EQ = 1 : 3.
Найдите площадь треугольника EPF.
С-5. В остроугольном треугольнике ABC (где AB > BC) проведены высоты AM и CN, точка O — центр описанной около треугольника ABC окружности. Известно, что величина угла ABC равна β, а площадь четырехугольника NOMB равна S. Найдите длину стороны AC.
С-6. В треугольнике ABC точка K на стороне AB и точка M на стороне AC расположены так, что выполняются соотношения AK : KB = 3 : 2 и AM : MC = 4 : 5. В каком отношении точка пересечения прямых KC и BM делит отрезок BM?
С-7. Внутри прямоугольного треугольника ABC (угол B прямой) взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника ABC. Длины отрезков AD и DC равны соответственно a и c. Найдите длину отрезка BD.
С-8. В выпуклом четырехугольнике ABCD на стороне CD взята точка E так, что отрезок AE делит четырехугольник ABCD на ромб и равнобедренный треугольник, отношение площадей которых равно Найдите величину угла BAD.
С-9. Высота трапеции ABCD равна 7, а длины оснований AD и BC равны соответственно 8 и 6. Через точку E, лежащую на стороне CD, проведена прямая BE, которая делит диагональ AC в точке O в отношении AO : OC = 3 : 2. Найдите площадь треугольника OEC.
С-10. Точки K, L, M делят стороны выпуклого четырехугольника ABCD в отношении AK : BK = CL : BL = CM : DM = 1 : 2. Известно, что радиус описанной около треугольника KLM окружности равен KL = 4, LM = 3 и KM < KL. Найдите площадь четырехугольника ABCD.
С-11. Продолжения сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке M, а продолжения сторон AB и CD — в точке O. Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольников AOD и BOC, если OA = 6, OD = 4, CD = 1.
С-12. В треугольнике ABC угол при вершине A равен 30°, а высоты BD и CE пересекаются в точке O. Найдите отношение радиусов окружностей, описанных около треугольников DEO и ABC.
С-13. Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найдите радиус описанной около треугольника окружности.
С-14. В остроугольном треугольнике ABC на высоте AD взята точка M, а на высоте BP — точка N так, что углы BMC и ANC — прямые. Расстояние между точками M и N равно а ∠MCN = 30°.
Найдите биссектрису CL треугольника CMN.
С-15. На сторонах AB, BC и AC треугольника ABC взяты точки D, E и F соответственно. Отрезки AE и DF проходят через центр вписанной в треугольник ABC окружности, а прямые DF и BC параллельны. Найдите длину отрезка BE и периметр треугольника ABC, если BC = 15, BD = 6, CF = 4.
С-16. В треугольнике ABC биссектриса BB' пересекает медиану AA' в точке O.
Найдите отношение площади треугольника BOA' к площади треугольника AOB', если AB : AC = 1 : 4.
С-17. В треугольнике ABC точка D лежит на AC, причем AD = 2DC. Точка E лежит на BC. Площадь треугольника ABD равна 3, площадь треугольника AED равна 1. Отрезки AE и BD пересекаются в точке O. Найдите отношение площадей треугольников ABO и OED.
С-18. В параллелограмме ABCD точки E и F лежат соответственно на сторонах AB и BC, M — точка пересечения прямых AF и DE, причем AE = 2BE, а BF = 3CF. Найдите отношение AM : MF.
С-19. В прямоугольнике ABCD на сторонах
AB и AD выбраны соответственно точки E и F так, что AE : EB = 3 : 1, AF : FD = 1 : 2. Найдите EO : OD, где O — точка пересечения отрезков DE и CF.
С-20. На стороне PQ треугольника PQR взята точка N, а на стороне PR — точка L, причем
NQ = LR. Точка пересечения отрезков QL и NR делит отрезок QL в отношении m : n, считая от точки Q. Найдите отношение PN : PR.
С-21. На сторонах острого угла с вершиной O взяты точки A и B. На луче OB взята точка M на расстоянии 3OA от прямой OA, а на луче OA — точка N на расстоянии 3OB от прямой OB. Радиус окружности, описанной около треугольника AOB, равен 3. Найдите MN.
С-22. В выпуклом пятиугольнике ABCDE диагонали BE и CE являются биссектрисами углов при вершинах B и C соответственно, ∠A = 35°, ∠D = 145°, S∆BCE = 11. Найдите площадь пяти­угольника ABCDE.
С-23. На основаниях AD и BC трапеции ABCD построены квадраты ADEF и BCGH, расположенные вне трапеции. Диагонали трапеции пересекаются в точке O. Найдите длину отрезка AD, если BC = 2, GO = 7, а GF = 18.
С-24. В треугольнике ABC известно, что AB = BC, а угол BAC равен 45°. Прямая MN пересекает сторону AC в точке M, а сторону BC — в точке N, причем AM = 2MC, а ∠NMC = 60°. Найдите отношение площади треугольника MNC к площади четырехугольника ABNM.
С-25. В треугольнике ABC взяты точка N на стороне AB, а точка M — на стороне AC. Отрезки CN и BM пересекаются в точке O, AN : NB = 2 : 3,
BO : OM = 5 : 2. Найдите CO : ON.

Ответы:

Садовничий Ю.