Решаем задачи по геометрии: углы в окружностях

Основные теоремы

Определение 1. Угловой величиной дуги называется отношение длины этой дуги к длине окружности, умноженное на 2π.

Теорема 1. Величина центрального угла равна угловой величине дуги, на которую он опирается.

Теорема 2. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается.
Следствие. Вписанные углы, опирающиеся на одну и ту же дугу или на равные дуги одной окружности, равны.

Теорема 3. Угол между касательной и хордой, выходящими из одной точки окружности, измеряется половиной угловой величины дуги, заключенной внутри этого угла (рис. 1).

Теорема 4. Угол, вершина которого расположена вне круга, измеряется полуразностью угловых величин дуг окружности этого круга, заключенных внутри угла (рис. 2).

Теорема 5. Угол, вершина которого расположена внутри круга, измеряется полусуммой угловых величин дуг, которые высекают из окружности круга стороны угла и их продолжения (рис. 3).

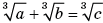
Теорема 6. Сумма противоположных углов четырехугольника, вписанного в окружность, равна π, и наоборот, если сумма противоположных углов выпуклого четырехугольника равна π, то вокруг этого четырехугольника можно описать окружность.

Теорема 7. Произведения длин отрезков двух пересекающихся хорд равны (см. рис. 3).

Теорема 8. Произведение длины отрезка секущей на длину ее внешней части есть величина постоянная, и она равна квадрату длины касательной, проведенной к окружности из той же точки (рис. 4).

Доказательства некоторых теорем

Доказательство теоремы 4. Рассмотрим сначала случай, когда лучи, образующие данный угол, пересекают окружность каждый в двух различных точках (рис. 5).

Обозначим через O вершину угла, а точки пересечения лучей и окружности через A, B, C и D (A между O и B, C между O и D). Тогда

Первое равенство верно, так как в треугольнике OBC внешний угол BCD равен сумме двух внутренних углов, с ним не смежных.
Пусть теперь один из лучей (например, OA) касается окружности в точке A, а другой пересекает ее в точках B и C; B между O и C (рис. 6).

Тогда

И наконец, пусть оба луча OA и OB касаются окружности в точках A и B (рис. 7).

Тогда треугольник OAB является равнобедренным, и

где дуга ACB — большая из дуг окружности, заключенных между точками A и B.

Доказательство теоремы 5. Пусть хорды AB и CD окружности пересекаются в точке O (рис. 8). Так как в треугольнике OBD внешний угол AOD равен сумме двух внутренних углов, с ним не смежных, то

Доказательство теоремы 8. Докажем сначала первую часть теоремы. Пусть OB и OD — две секущие к окружности, а OA и OC — соответственно их внешние части. Так как углы ABC и ADC равны (как вписанные, опирающиеся на одну и ту же дугу), то треугольники AOD и BOC подобны (по двум углам). Следовательно,

Пусть теперь OK — касательная к окружности, а OB — секущая (OA ее внешняя часть) (рис. 9).

Так как угол OKA равен половине угловой величины дуги KA (как угол между касательной и хордой), а угол KBA равен половине угловой величины дуги KA (как вписанный, опирающийся на эту дугу), то ∠OKA = ∠KBA, и треугольник OKA подобен треугольнику KOB (по двум углам). Имеем:

Решения задач

Задача 1. Правильный треугольник ABC со стороной, равной 3, вписан в окружность. Точка D лежит на окружности, причем длина хорды AD равна (рис. 10). Найти длины хорд BD и CD.

Решение.

Легко видеть, что радиус окружности, описанной около правильного треугольника со стороной a, равен
начит, радиус данной окружности равен . Пусть O — центр данной окружности. В треугольнике AOD все стороны равны. Поэтому ∠DAO = 60°. Кроме того, так как треугольник ABC — правильный, то ∠OAC = 30°.
Значит, ∠DAC = 90°, и треугольник DAC — прямоугольный. Следовательно, CD — диаметр окружности, и Значит, и треугольник BCD прямоугольный, откуда по теореме Пифагора находим, что Ясно, что при переобозначении точек B и C получим, что

Ответ: и

Задача 2. Окружность радиуса R проходит через вершины A и B треугольника ABC и касается прямой AC в точке A (рис. 11). Найти площадь треугольника ABC, зная, что ∠ABC = β, ∠CAB = α.

Решение. Угол α между касательной AC и хордой AB, выходящими из точки A окружности, равен половине угловой величины дуги AB и, значит, равен любому вписанному углу, опирающемуся на ту же дугу. Поэтому мы можем применить теорему синусов: AB = 2Rsin α.
Рассмотрим треугольник ABC, к которому также применим теорему синусов:

Следовательно,

Ответ:

Задача 3. Вокруг треугольника ABC описана окружность. Медиана AD продолжена до пересечения с этой окружностью в точке E (рис. 12). Известно, что AB + AD = DE, угол BAD равен 60° и AE = 6. Найти площадь треугольника ABC.

Решение. Пусть AB = x, AD = y, тогда, согласно условию задачи, DE = x + y. Так как в окружности произведения отрезков двух пересекающихся хорд равны, имеем:
AD∙DE = BD∙DC ⇔
Применим к треугольнику ABD теорему косинусов:
BD2 = AB2 + AD2 – 2AB∙AD∙cos ∠BAD ⇔
⇔ ⇔ x2 = 2xy ⇔ x = 2y.
Условие AE = 6 дает равенство x + 2y = 6. Подставляя в него x = 2y, находим: x = 3. Искомая площадь равна

Ответ:

Задача 4. На стороне AC остроугольного треугольника ABC взята точка D так, что AD = 1,
DC = 2 и BD является высотой треугольника ABC. Окружность радиуса 2, проходящая через точки A и D, касается в точке D окружности, описанной около треугольника BDC (рис. 13). Найти площадь треугольника ABC.

Решение. Треугольник BCD — прямоугольный, поэтому центр описанной около него окружности есть середина M стороны BC. Пусть O — центр окружности радиуса 2, проходящей через A и D. Так как данные окружности касаются, то точки O, D, M лежат на одной прямой. А из равенства углов ADO и CDM, в силу равнобедренности треугольников ADO и CDM, следует подобие этих треугольников. Значит, DM = 4 и BC = 2 DM = 8.Применив теорему Пифагора к треугольнику BCD, получим, что Следовательно,

Ответ:

Задача 5. Дан треугольник ABC, в котором
BC = 5. Окружность проходит через вершины B и C и пересекает сторону AC в точке K так, что
CK = 3, KA = 1. Известно, что косинус угла ACB равен (рис. 14). Найти отношение радиуса данной окружности к радиусу окружности, вписанной в треугольник ABK.

Решение. Применим к треугольнику ABC теорему косинусов:
AB2 = BC2 + AC2 – 2BC∙AC∙cos ∠ACB = 9 ⇒
⇒ AB = 3.
Следовательно, треугольник ABC — прямоугольный (так как его стороны равны 3, 4, 5). Треугольник ABK также прямоугольный, применив к нему теорему Пифагора, получим, что Значит, радиус вписанной в треугольник ABK окружности равен

Окружность, данная в условии задачи, описана около треугольника BCK. По теореме синусов ее радиус равен

Тогда искомое отношение равно

Ответ:

Задача 6. В треугольнике ABC известны стороны AB = 6, BC = 4, AC = 8. Биссектриса угла C
пересекает сторону AB в точке D. Через точки A, D, C проведена окружность, пересекающая сторону BC в точке E (рис. 15). Найти площадь треугольника ADE.

Решение. Биссектриса CD угла ACB делит сторону AB на отрезки, пропорциональные прилежащим сторонам, поэтому AD = 4 и BD = 2. Далее, углы DAE и DCE равны, как опирающиеся на одну и ту же дугу, и аналогично равны углы AED и ACD. Но ∠ACD = ∠DCE, поэтому все четыре названных угла равны. Следовательно, треугольник ADE — равнобедренный и DE = 4.
Найдем синус угла ADE. Так как четырехугольник ADEC вписан в окружность, то
∠ADE + ∠ACE = 180°, sin ∠ADE = sin ∠ACE.
Применим к треугольнику ABC теорему косинусов:

Значит,

Ответ:

Задача 7. Вокруг треугольника ABC со сторонами AC = 20 и углом B, равным 45°, описана окружность. Через точку C проведена касательная к окружности, пересекающая продолжение стороны AB за точку A в точке D (рис. 16). Найти площадь треугольника BCD.

Решение. Угол ABC равен половине угловой величины дуги AC, как вписанный угол, опирающийся на эту дугу. Угол ACD также равен половине угловой величины дуги AC, как угол между касательной и хордой. Следовательно, эти углы равны, и треугольники DBC и DCA подобны по двум углам. Площади этих треугольников относятся как квадрат коэффициента подобия. Найдем этот коэффициент, он равен BC : AC. Пусть BC = 10x, тогда, применив к треугольнику ABC теорему косинусов, получим:

Значит,

Поэтому



С другой стороны, легко вычислить

Значит,

Ответ:

Задача 8. В окружность радиуса 17 вписан четырехугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8 и 9 от центра окружности (рис. 17). Найти длины сторон четырехугольника.

Решение. Обозначим исходный четырех­угольник через ABCD таким образом, чтобы точка B лежала на меньшей дуге AC, а точка A лежала на меньшей дуге BD. Пусть O — центр окружности, OQ и OP — перпендикуляры, опущенные из центра окружности на хорды AC и BD соответственно, M — точка пересечения AC и BD. Тогда AQ = QC, BP = PD, OQMP — прямоугольник со сторонами OQ = PM = 8 и
OP = QM = 9. Применим к треугольнику COQ теорему Пифагора:

Аналогично из треугольника ODP получим, что

Значит,

Находим стороны четырехугольника ABCD, пользуясь теоремой Пифагора:

Ответ:

Задача 9. Пятиугольник ABCDE вписан в окружность единичного радиуса (рис. 18).
Известно, что и BC = CD. Чему равна площадь пятиугольника?

Решение. Пусть O — центр данной окружности. Так как стороны треугольника AOB равны 1, 1 и то этот треугольник прямоугольный, и угол AOB равен . Поскольку угол ABE равен , то угол AOE также равен , и BE — диаметр окружности. Угол EBD равен следовательно, угол EOD равен а так как BC = CD, то
Итак, пятиугольник ABCDE состоит из двух прямоугольных и трех равносторонних треугольников. Его площадь равна

Ответ:

Задача 10. Выпуклый четырехугольник ABCD вписан в окружность. Диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке K (рис. 19). Найти длину отрезка KC, если BC = 4, а AK = 6.

Решение. Так как AC — биссектриса угла BAD, то угол BAC равен углу CAD. С другой стороны, углы CAD и CBD равны (как вписанные, опирающиеся на одну и ту же дугу). Значит, угол BAC равен углу CBK. Следовательно, треугольник ABC подобен треугольнику BCK (по двум углам). Имеем:

Ответ: 2.

Задачи для самостоятельного решения

С-1. В треугольнике ABC имеем: AB = 20, AC = 24. Известно, что вершина C, центр вписанного в треугольник ABC круга и точка пересечения биссектрисы угла A со стороной BC лежат на окружности, центр которой находится на стороне AC. Найдите радиус описанной около треугольника ABC окружности.
С-2. Дан прямоугольный треугольник ABC с прямым углом при вершине C. Угол CAB равен α. Биссектриса угла ABC пересекает катет AC в точке K. На стороне BC как на диаметре построена окружность, которая пересекает гипотенузу AB в точке M. Найдите угол AMK.
С-3. На плоскости даны две пересекающиеся окружности. Первая имеет центр в точке O1 и радиус, равный 4, вторая — центр в точке O2 и радиус, равный Отрезок O1O2 пересекает обе окружности, а угол KO1O2 равен 30° (где K — одна из точек пересечения окружностей). Вершина A равностороннего треугольника ABC является точкой пересечения второй окружности и отрезка O1O2, а сторона BC — хордой первой окружности, перпендикулярной к прямой O1O2. Найдите площадь треугольника ABC, если известно, что AB < 4.
С-4. В окружность вписан четырехугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке E. Прямая, проходящая через точку E и перпендикулярная к AB, пересекает сторону CD в точке M. Докажите, что EM — медиана треугольника CED, и найдите ее длину, если AD = 8, AB = 4 и ∠CDB = α.
С-5. Трапеция ABCD вписана в окружность (BC C AD). На дуге CD взята точка E и соединена со всеми вершинами трапеции. Кроме того, известно, что ∠CED = 120° и ∠ABE – ∠BAE = α. Для треугольника ABE найдите отношение периметра к радиусу вписанной окружности.
С-6. В треугольнике ABC известно, что BC = 4. Кроме того центр окружности, проведенной через середины сторон треугольника, лежит на биссектрисе угла C. Найдите AC.
С-7. В треугольнике ABC на сторонах AB и AC выбраны соответственно точки B1 и C1 таким образом, что AB1 : AB = 1 : 3 и AC1 : AC = 1 : 2. Через точки A, B1 и C1 проведена окружность. Через точку B1 проведена прямая, пересекающая отрезок AC1 в точке D, а окружность — в точке E.
Найдите площадь треугольника B1C1E, если AC1 = 4, AD = 1, DE = 2, а площадь треугольника ABC равна 12.
С-8. Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке E. На прямой AC взята точка M, причем ∠DME = 80°, ∠ABD = 60°, ∠CBD = 70°. Где находится точка M: на диагонали или на ее продолжении? Ответ обоснуйте.
С-9. Через центр окружности, описанной около треугольника ABC, проведены прямые, перпендикулярные сторонам AC и BC. Эти прямые пересекают высоту CH треугольника или ее продолжение в точках P и Q. Известно, что CP = p, CQ = q. Найдите радиус окружности, описанной около треугольника ABC.
С-10. На стороне AB треугольника ABC как на диаметре построена окружность, пересекающая стороны AC и BC в точках D и E соответственно. Прямая DE делит площадь треугольника ABC пополам и образует с прямой AB угол 15°. Найдите углы треугольника ABC.
С-11. Окружность касается сторон угла с вершиной O в точках A и B. На этой окружности внутри треугольника AOB взята точка C. Расстоя­ния от точки C до прямых OA и OB равны соответственно a и b. Найдите расстояние от точки C до хорды AB.
С-12. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке E. Вокруг треугольника ECB описана окружность, а касательная к этой окружности, проведенная в точке E, пересекает прямую AD в точке F таким образом, что точки A, D и F лежат последовательно на этой прямой. Известно, что AF = a, AD = b. Найдите EF.
С-13. В четырехугольнике ABCD диагонали AC и BD перпендикулярны и пересекаются в точке P. Длина отрезка, соединяющего вершину C с точкой M, являющейся серединой отрезка AD, равна Расстояние от точки P до отрезка BC равно и AP = 1. Найдите длину отрезка AD, если известно, что вокруг четырехугольника ABCD можно описать окружность.
С-14. В окружности проведены диаметр MN и хорда AB, параллельная диаметру MN. Касательная к окружности в точке M пересекает прямые NA и NB соответственно в точках P и Q. Известно, что MP = p, MQ = q. Найдите MN.
С-15. Через вершины A и B треугольника ABC проведена окружность, пересекающая стороны BC и AC в точках D и E соответственно. Площадь треугольника CDE в 7 раз меньше площади четырехугольника ABDE. Найдите DE и радиус окружности, если AB = 4 и ∠C = 45°.
С-16. Через точку L окружности проведена касательная и хорда LM длины 5. Хорда MN параллельна касательной и равна 6. Найдите радиус окружности.
С-17. Диагонали вписанного в окружность четырехугольника ABCD пересекаются в точке E, причем BD = 6 и AD∙CE = DC∙AE. Найдите площадь четырехугольника ABCD.
С-18. В треугольнике ABC известно, что длина AB равна 3, Хорда KN окружности, описанной около треугольника ABC, пересекает отрезки AC и BC в точках M и L соответственно. При этом ∠ABC = ∠CML, площадь четырехугольника ABLM равна 2, а длина LM равна 1. Найдите высоту треугольника KNC, опущенную из вершины C, и его площадь.
С-19. В треугольнике ABC точка D лежит на стороне BC, прямая AD пересекается с биссектрисой угла ACB в точке O. Известно, что точки C, D и O лежат на окружности, центр которой находится на стороне AC, AC : AB = 3 : 2, а величина угла DAC в три раза больше величины угла DAB. Найдите косинус угла ACB.
С-20. Окружность, вписанная в равнобедренный треугольник ABC, касается основания AC в точке D и боковой стороны AB в точке E. Точка F — середина стороны AB, а точка G — точка пересечения окружности и отрезка FD, отличная от D. Касательная к данной окружности, проходящая через точку G, пересекает сторону AB в точке H. Найдите угол BCA, если известно, что FH : HE = 2 : 3.
С-21. На отрезке AB взята точка C и на отрезках AB и CB как на диаметрах построены окружности. Хорда AM большей окружности касается меньшей окружности в точке D. Прямая BD пересекает большую окружность в точке N. Известно, что ∠DAB = a, AB = 2R. Найдите площадь четырехугольника ABMN.
С-22. В треугольнике ABC биссектрисы AD и BL пересекаются в точке F. Величина угла LFA равна 60°.
1) Найдите величину угла ACB.
2) Вычислите площадь треугольника ABC, если ∠CLD = 45° и AB = 2.
С-23. Две окружности пересекаются в точках A и B. Через точку B проведена прямая, пересекающая окружности в точках C и D, лежащих по разные стороны от прямой AB. Касательные к этим окружностям в точках C и D пересекаются в точке E. Найдите AD, если AB = 15, AC = 20 и AE = 24.
С-24. В трапеции ABCD с боковыми сторонами AB = 9 и CD = 5 биссектриса угла D пересекает биссектрисы углов A и C в точках M и N соответственно, а биссектриса угла B пересекает те же две биссектрисы в точках L и K, причем точка K
лежит на основании AD. В каком отношении прямая LN делит сторону AB, а прямая MK — сторону BC? Найдите отношение MN : KL, если LM : KN = 3 : 7.

Ответы:

 

Садовничий Ю.